Geohash-EAS - a Modified Geohash Geocoding System with Equal-Area Spaces
Abstract
The Geohash geocoding system is a way of geographic coordinates coding by converting the latitude and longitude pair into an alphanumeric character string where each subsequent symbol increases the position accuracy. The algorithm for separating the map onto individual spaces uses simple arithmetic operations and as a result, the spaces have different surface areas - in the proportions near 1:2.4 for spaces located between latitude 0°-45° and those located between latitude 45°-90°. All subsequent divisions onto subspaces inherit this disproportion in surface areas and the trend is getting worse. The area of subspace ‘sb’ (same as ‘s0’) where is located most of the Kenya is 2.9 times larger than the area of subspace ‘uk’ (same as ‘uh’) where is located northern parts of Norway, Sweden and Finland. In this publication, in order to create spaces of the same surface areas, a modification of the algorithm dividing Earth map onto spaces, is described. The new system, where all spaces with same string length of the name have equal surface area, we called it Geohash-EAS.
Keywords: Geohash, geocoding, map, equal-area spaces, Geohash-EAS
INTRODUCTION
The geohash geocoding system is used in a variety of database and system management systems - REDIS [1, 2], MongoDB, MySQL, Lucene, Sorl, Cassandra, Memcached, CouchBase, HBase, PostgreSQL (PostGIS), DynamoDB, etc. It is a way to encode geographic coordinates by converting the latitude and longitude pair into a single alphanumeric string that indicates a space from the Earth’s surface. Each subsequent string symbol reduces the size of the space and increases the accuracy of the location. The Geohash string can be used as a unique identifier for spatial indexing and quick search.
Converting geographic coordinates into a string using the original Geohash system [3] is done by initially dividing the map into 4 rows and 8 columns. The resulting 32 spaces are named from NW to SE direction with symbols from the alphanumeric character set “bcfguvyz89destwx2367kmqr0145hjnp”. An example of the initial map division into 32 spaces is given on Figure 1.
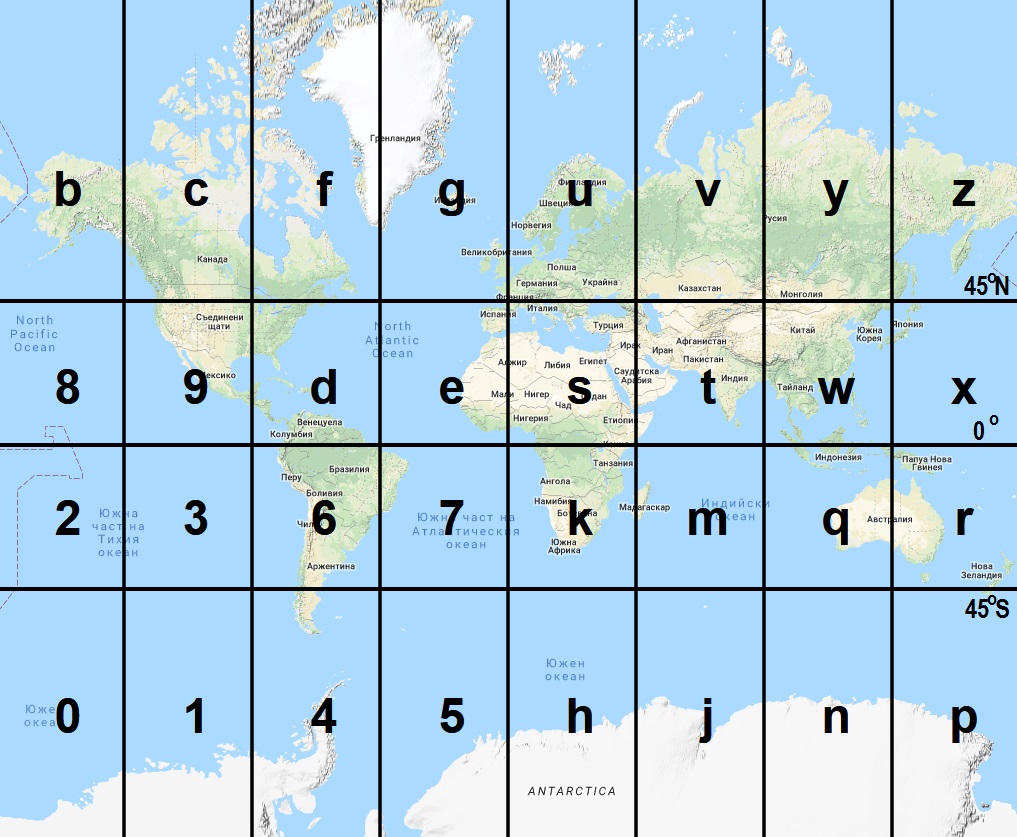
Figure 1. Initial Earth map division into 32 spaces using the original Geohash system. Google Map and Google Web Mercator projection are used in this visualisation.
Figure 1. Initial Earth map division into 32 spaces using the original Geohash system. Google Map and Google Web Mercator projection are used in this visualisation.
For each space, the partitioning process can be repeated and subdivided into smaller 32 subspaces, and the Geohash system special feature is that if 4 rows and 8 columns divisions are made then the next division must be 8 rows and 4 columns. Then the resulting subspaces are named from NW to SE direction with symbols from the alphanumeric character set “prxznqwyjmtvhksu57eg46df139c028b”. The sequences in the character sets are chosen in a special way that is not relevant to the current issue and will therefore not be considered further. The subsequent division of spaces “s” and “u” into 32 subspaces is showed on Fig.2.
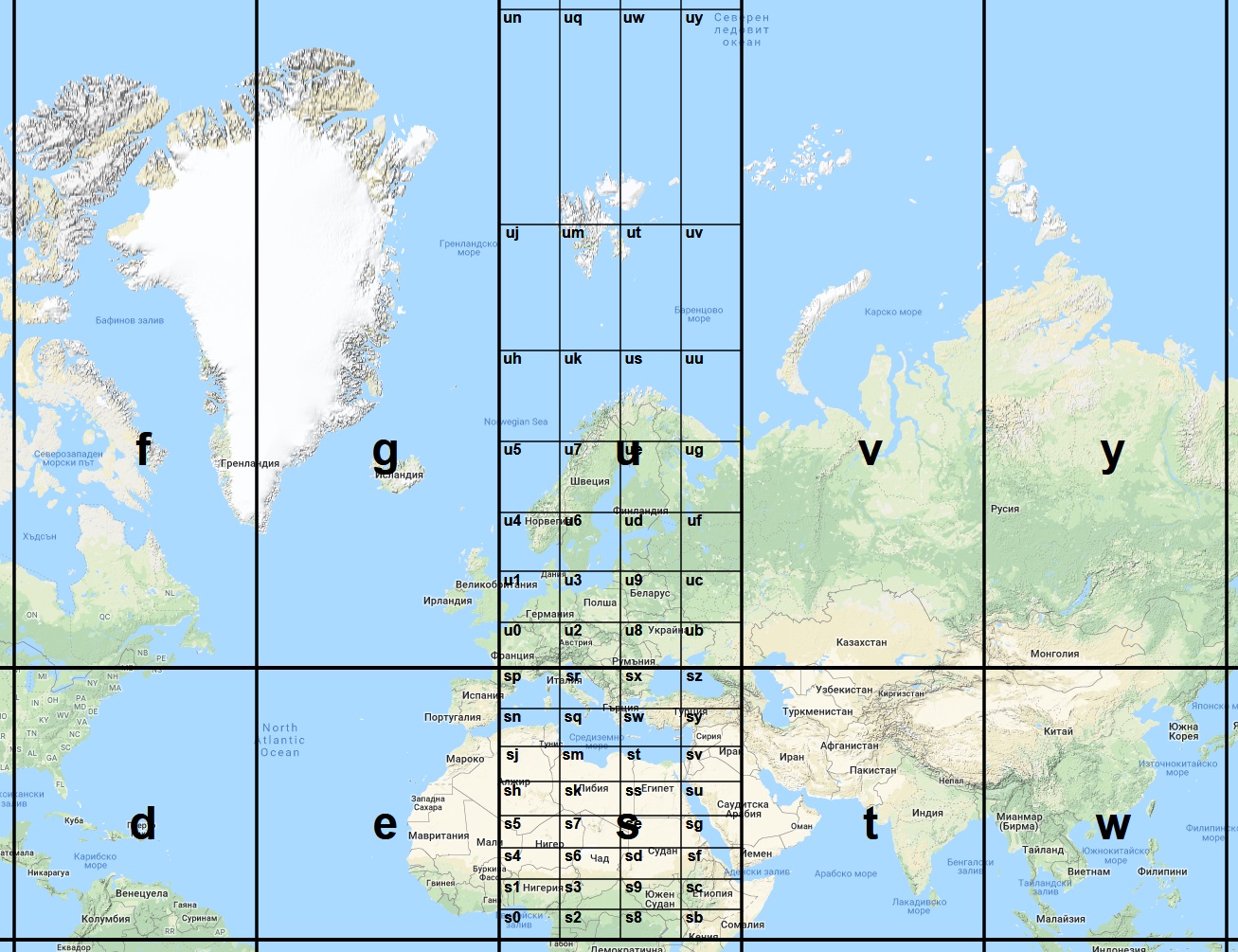
Figure 2. Subsequent division of spaces ’s’ and ‘u’ into 32 subspaces using the original Geohash system.
Each division of a space into smaller subspaces results in adding a new symbol to the Geohash string. The number of characters in the string is directly related to the accuracy of the location. If characters are removed from the end of the string, the effect is the same as removing digits from the end of the numbers which indicating the latitude and longitude.
When dividing the map into subspaces, the following rules are used: latitude is a number in the range -90°; +90°, and the longitude is a number in the range -180°; +180°. These numbers represent angles in degrees measured against the center of the sphere we consider to represent the Earth. Latitude is the angle formed by the plane crossing the equator and the line connecting the center of the sphere and the point of the sphere. The longitude is the angle between the plane of the prime (Greenwich) meridian and the meridian plane on which is the point of the sphere. The both last mentioned planes pass through the center of the sphere and their cross section represents the earth axis. So in the first step the S to N range [-90°; +90°] is divided into 4 equal parts with step 45° and the W to E range [-180°; +180°] is divided into 8 equal parts with step 45°.
The use of Geohash allows quick localization of objects that are close to one another. In the majority of cases, they will have the same Geohash string prefixes. Similar objects could be retrieved with simple fast-executing SQL queries. For example, the following query will retrieve from a database objects located in a large area around the city of Brussel together with its suburbs:
SELECT * FROM some_table WHERE geohash LIKE 'u151%';
The following query will retrieve from a database objects located in the small area around the Atomium monument in Brussel:
SELECT * FROM some_table WHERE geohash LIKE 'u151dc1%';
MySQL have various functions, which also could be used in such cases [4].
THE MAIN PROBLEM WITH THE EXISTING APPROACH
The division of the map into subspaces could easily be done by dividing numbers by half and this method of separating the map uses simple arithmetic operations. As a result, each space on Fig.1 has dimensions 45° width and 45° height, but the dimensions measured in m, km, miles and so on, are not such equal. In reality, the spaces are not only of different sizes but also have different areas.
For example, the width in meters at the bottom of the space “s” is equal to the height (for simplicity we assume that the Earth is sphere) but is less than the width at the top of this spherical rectangle. On the Earth poles all meridians are joined (intersected) at one point and therefore the width in meters at the top end of the space “u” (and the remaining spaces on the same row) will be infinitely tending to zero. Assuming that the radius of the Earth, which we accepted as a sphere, is around 6371 km, we can say with an acceptable degree of accuracy that: 1° of the Equator equals 111.2 km for the space height and width, so the bottom of the space “s” will be 5003.8 km (45° x 111.2 km). The height of space “s” also will be 5003.8 km. But 1° of the 45° parallel will be only 78.6 km (2π x [6371 km x cos(45°)] / 360°) and the width of the top side of the space “s” will be 3538.2 km (45° x 78.6 km).
The width of the bottom side of space “u” will be the same as the width of the top side of space “s” - also 3538.2; the height will be the same as the height of space “s” - 5003.8 km; but the width of the top side of space “u” will be zero. Unlike the space “s” which is spherical rectangle, the space “u” is spherical triangle. On maps using Google Web Mercator projection, this is of course not visible and obvious. As a result, the surface area [5] of the space “s” is 22.5 million km2 (2π x [6371 km]2 x [sin(45°) - sin(0°)] / 8 spaces) and the surface area of the space “u” is only 9.3 million km2 (2π x [6371 km]2 x [sin(90°) - sin(45°)] / 8 spaces). The area of space “s” is around 2.4 times larger than the area of space “u”.
As mentioned earlier, after dividing of the angles representing the latitude in equal parts, the spaces on different rows have different areas. This difference in the initial division of the northern hemisphere is illustrated in Fig. 3. The area of spaces in the top row is 29.3% of the total area of the northern hemisphere and the area of the bottom row is 70.7%. All subsequent divisions onto subspaces inherit this disproportion in surface areas and the trend is getting worse. For example the area of subspace “sb” (same as “s0”) where is located most of the Kenya is 2.9 times larger than the area of subspace “uk” (same as “uh”) where is located northern parts of Norway, Sweden and Finland (Table 1).
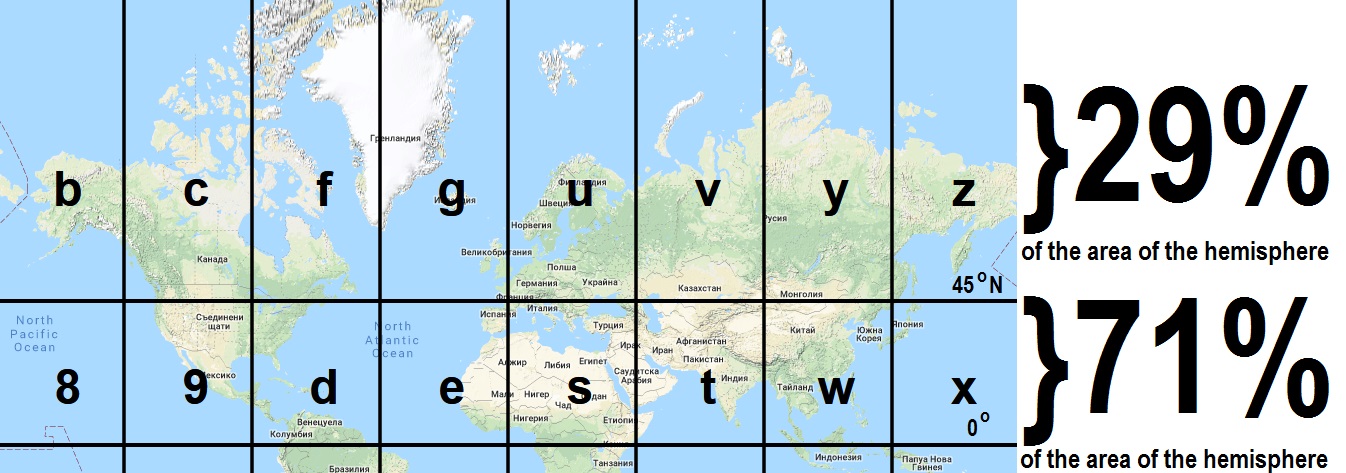
Figure 3. Disproportions in surface areas between the two rows with spaces in northern hemisphere as the result of using the original Geohash system.
The variation of surface areas of spaces in sometimes creates inconvenience and is undesirable. In such cases, the surface area of all spaces with similar string length of the names should be equal [6]. With the existing Geohash system this is not possible and it should be modified. We suggest a new system - Geohash-EAS where the EAS abbreviation means “Equal-Area Spaces”.
Table 1. Coordinates and area of some spaces using Geohash system.
| Space name | LatitudeS | LatitudeN | LongitudeW | LongitudeE | Area[km2] |
|---|---|---|---|---|---|
| s | 0° | 45°N | 0° | 045°E | 22 541 877 |
| u | 45°N | 90°N | 0° | 045°E | 9 337 151 |
| s0 | 0° | 5.625°N | 0° | 011.25°E | 781 173 |
| s1 | 5.625°N | 11.25°N | 0° | 011.25°E | 773 650 |
| s4 | 11.25°N | 16.875°N | 0° | 011.25°E | 758 676 |
| s5 | 16.875°N | 22.5°N | 0° | 011.25°E | 736 396 |
| sh | 22.5°N | 28.125°N | 0° | 011.25°E | 707 024 |
| sj | 28.125°N | 33.75°N | 0° | 011.25°E | 670 842 |
| sn | 33.75°N | 39.375°N | 0° | 011.25°E | 628 201 |
| sp | 39.375°N | 45°N | 0° | 011.25°E | 579 509 |
| u0 | 45°N | 50.625°N | 0° | 011.25°E | 525 236 |
| u1 | 50.625°N | 56.25°N | 0° | 011.25°E | 465 905 |
| u4 | 56.25°N | 61.875°N | 0° | 011.25°E | 402 087 |
| u5 | 61.875°N | 67.5°N | 0° | 011.25°E | 334 397 |
| uh | 67.5°N | 73.125°N | 0° | 011.25°E | 263 487 |
| uj | 73.125°N | 78.75°N | 0° | 011.25°E | 190 038 |
| un | 78.75°N | 84.375°N | 0° | 011.25°E | 114 760 |
| up | 84.375°N | 90°N | 0° | 011.25°E | 38 377 |
COMPUTATIONAL DETAILS OF GEOHASH-EAS SYSTEM
In order for the converting from geographic coordinates to Geohash-EAS to be as fast as possible, the calculations should be kept as simple as possible. There is no change in the way of calculations of borders longitude of spaces. The calculation of borders latitude of spaces is quite different. Instead of dividing in equal parts, a much complicated formula should be used. After transformations of the spherical cap formula, we derived the following formula:
lat = arcsin( 2r / R )
, where:
lat - the latitude of the space border nears to the Equator (south border in northern hemisphere, north border in southern hemisphere). For the latitude near the pole the latitude of the next space towards the pole should be calculated, since both spaces share a common border.
R - number of rows. Depends on the string length: 1 char - 4 rows, 2 chars - 32 rows, 3 chars - 128, 4 chars - 1024, 5 - 4096, 6 - 32768, 7 - 131072 and so on.
r - the row number in the hemisphere, counted from the Equator and starting from 0. The row number in northern hemisphere is a positive number and negative in the southern.
By using such approach, the areas of all corresponding spaces will be the same (Fig. 4).
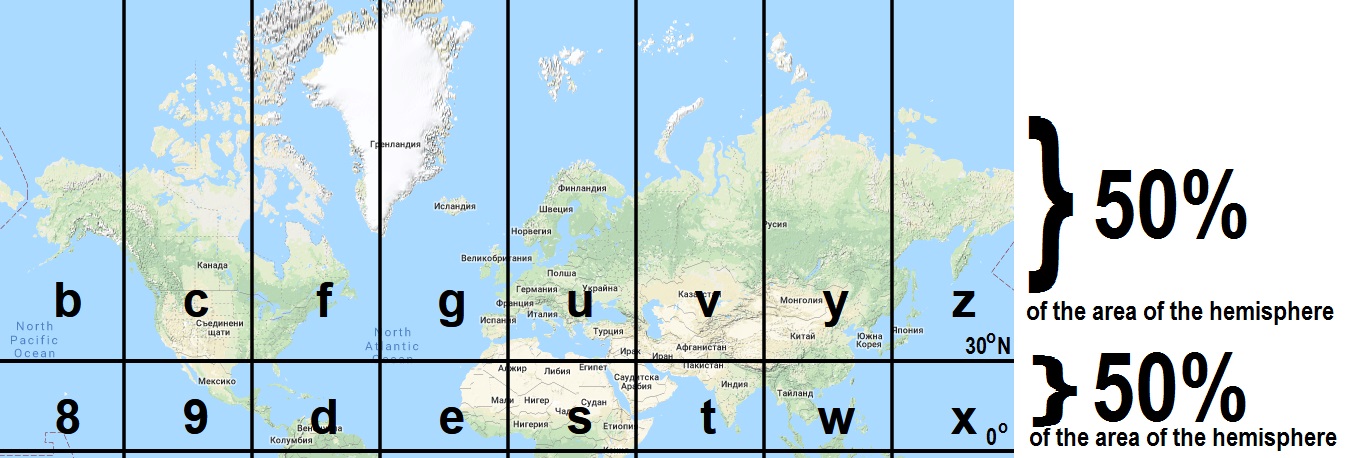
Figure 4. The surface areas between the two rows with spaces in northern hemisphere when the new Geohash-EAS system is used.
For example, the calculation of border latitudes of space “k” (covering Central and Middle Africa, Fig.5) using the Geohash-EAS system will be as follows. For the border close to the Equator: R = 4, r = 0, hence lat1 = arcsin(0) = 0°. For the latitude of the border close to the pole (in this case - South pole) we have to find the latitude of the next space towards the pole - the space “h”: R = 4 (since the string length is 1 char), r = -1 (since it is in the southern hemisphere), hence lat2 = arcsin(-0.5) = -30° = 30°S.
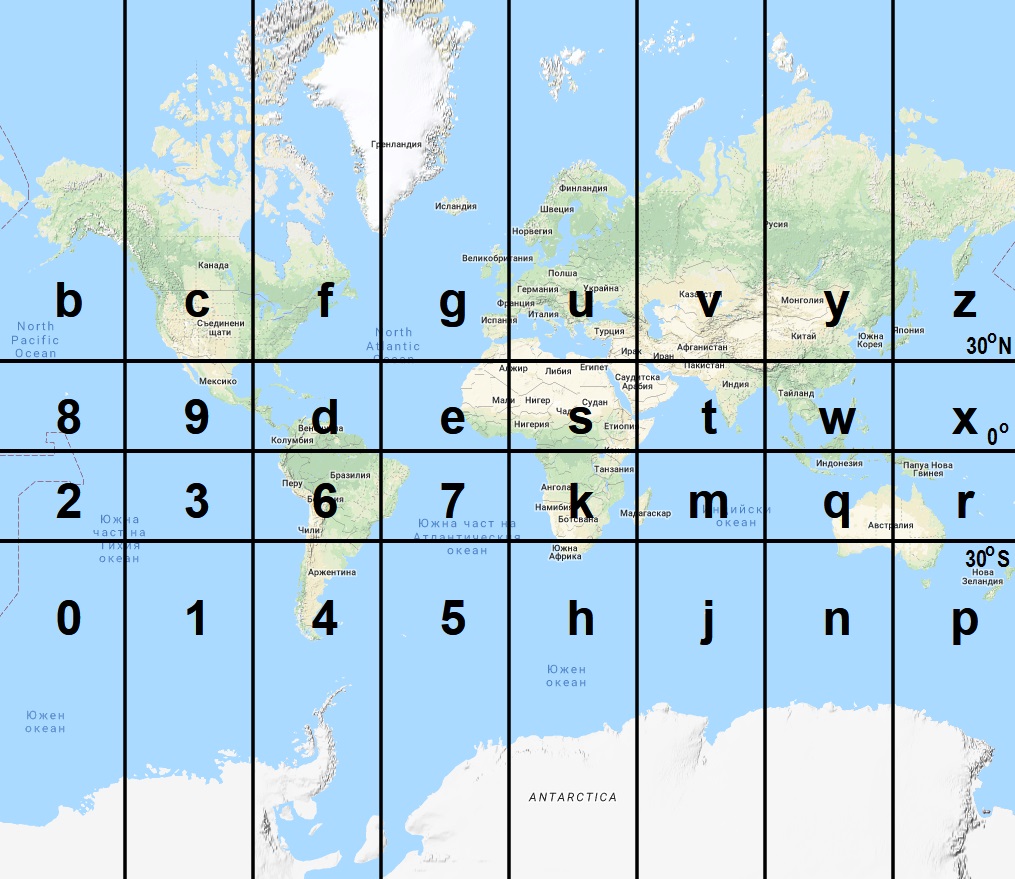
Figure 5. Initial Earth map division into 32 spaces using the Geohash-EAS system.
The calculation of border latitudes of space “uh” (covering Benelux countries, Fig.6) using the Geohash-EAS system will be as follows. For the border close to the Equator: R = 32 (since the string length is 2 chars), r = +12 (since it is in the northern hemisphere and rows counting starts from 0), hence lat1 = arcsin(+0.75) = +48.59° = 48.590N. For the latitude of the border close to the pole (in this case - North pole) we have to find the latitude of the next space towards the pole - the space “uj”: R = 4, r = +13, hence lat = arcsin(+0.8125) = +54.341° = 54.341°N.
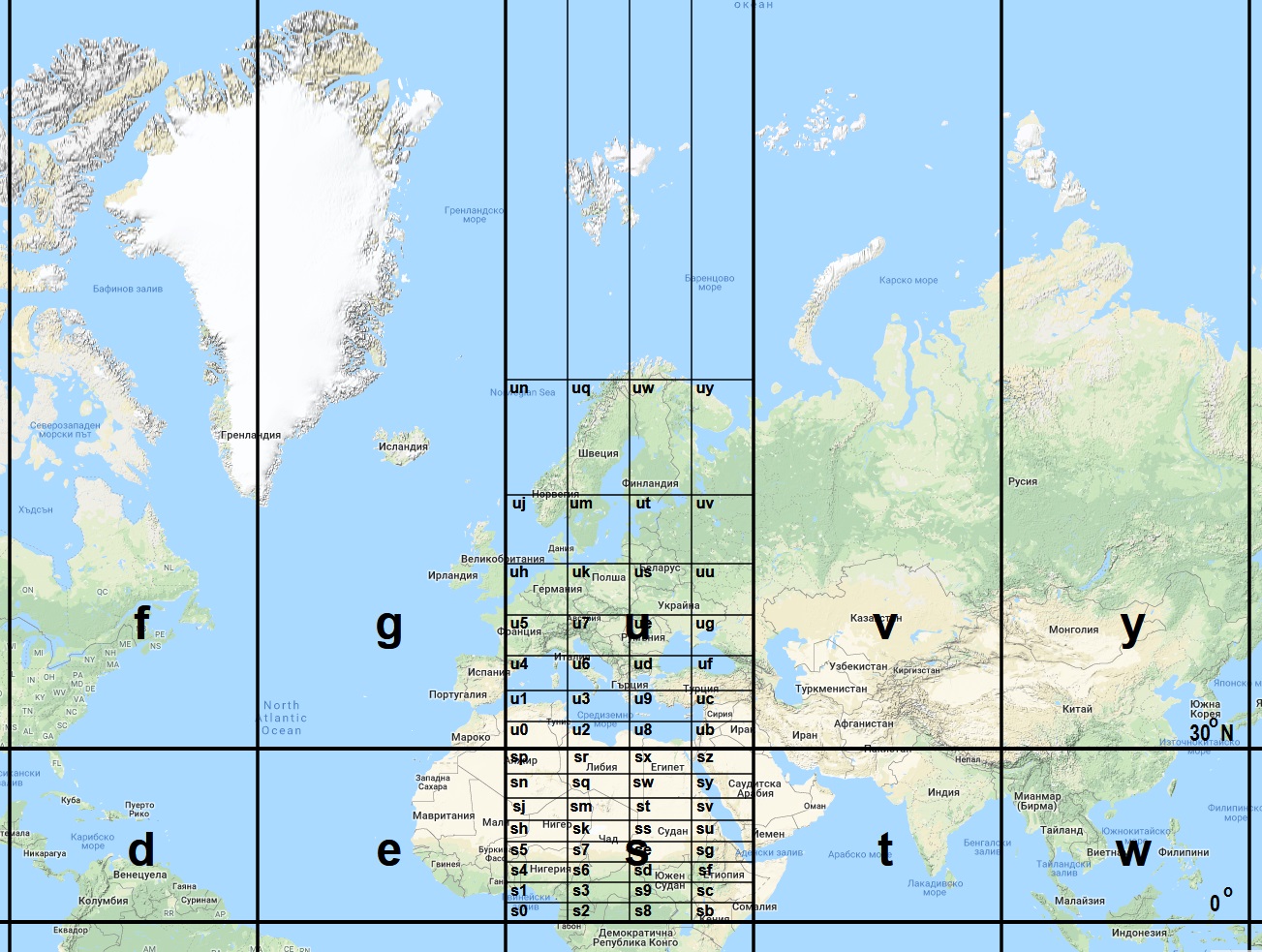
Figure 6. Subsequent division of spaces ’s’ and ‘u’ into 32 subspaces using the new Geohash-EAS system.
The coordinates of subspaces in the first column of spaces “s” and “u” using this calculation approach are presented on Table 2.
Table 2. Coordinates and area of some spaces using the new Geohash-EAS system.
| Space name | LatitudeS | LatitudeN | LongitudeW | LongitudeE | Area[km2] |
|---|---|---|---|---|---|
| s | 0° | 30°N | 0° | 045°E | 15 939 515 |
| u | 30°N | 90°N | 0° | 045°E | 15 939 515 |
| s0 | 0°N | 3.583°N | 0° | 011.25°E | 498 110 |
| s1 | 3.583°N | 7.181°N | 0° | 011.25°E | 498 110 |
| s4 | 7.181°N | 10.807°N | 0° | 011.25°E | 498 110 |
| s5 | 10.807°N | 14.478°N | 0° | 011.25°E | 498 110 |
| sh | 14.478°N | 18.210°N | 0° | 011.25°E | 498 110 |
| sj | 18.210°N | 22.024°N | 0° | 011.25°E | 498 110 |
| sn | 22.024°N | 25.944°N | 0° | 011.25°E | 498 110 |
| sp | 25.944°N | 30°N | 0° | 011.25°E | 498 110 |
| u0 | 30°N | 34.229°N | 0° | 011.25°E | 498 110 |
| u1 | 34.229°N | 38.682°N | 0° | 011.25°E | 498 110 |
| u4 | 38.682°N | 43.433°N | 0° | 011.25°E | 498 110 |
| u5 | 43.433°N | 48.590°N | 0° | 011.25°E | 498 110 |
| uh | 48.590°N | 54.341°N | 0° | 011.25°E | 498 110 |
| uj | 54.341°N | 61.045°N | 0° | 011.25°E | 498 110 |
| un | 61.045°N | 69.636°N | 0° | 011.25°E | 498 110 |
| up | 69.636°N | 90°N | 0° | 011.25°E | 498 110 |
Since calculating arcsin could be a computation intensive task, it is a good idea to implement caching (with or without pre-calculations). Already calculated values is stored in the cache and thus finding corresponding latitudes is considerably faster. For approximate calculations, next formula could be used [7]:
arcsin(X) = π/2 - (1-X)0.5(a0 + a1X + a2X2 + a3X3)
, where:
a0 = 1.5707288
a1 = -0.2121144
a2 = 0.0742610
a3 = -0.0187293
CONCLUSION
The algorithm for separating the map onto individual spaces, used by the original Geohash system, is simple and fast, but as a result, the spaces from different rows have different surface areas. The disproportion reaches 2.9 times difference in the area in spaces near the Equator and near the northern parts of Europe or North America. Even for spaces on 45°N the disproportion is around 1.3-1.5 times in such way so area of spaces closer to the Equator is larger. In some cases this is inconvenient and the surface area of all spaces should be equal. The proposed method for separating the map onto individual spaces includes using of arcsin for calculations. Since this creates spaces with different coordinates and sizes compared to the original Geohash system, a name Geohash-EAS is used. The abbreviation “EAS” stands for “Equal-Area Spaces”. All spaces described with 1 char have same areas - around 15 939 515 km2. All spaces described with 2 chars also have same areas - exactly 1⁄32 of the area with string length of 1 char - 498 110 km2 and so on. In this way, by division of 32 the areas of spaces with string length of 3, 4, 5 and more chars could be easily calculated.
REFERENCES
[1] Bird G., Blazingly Fast Geospatial Queries with Redis, https://developer.ibm.com/clouddataservices/2016/11/16/blazingly-fast-geospatial-queries-with-redis/, (retrieved 20.04.2018)
[2] GEOHASH – Redis, https://redis.io/commands/geohash, (retrieved 20.04.2018)
[3] Geohash - geohash.org, http://geohash.org/, (retrieved 20.04.2018)
[4] MySQL 8.0 Reference Manual, 12.15.10 Spatial Geohash Functions, https://dev.mysql.com/doc/refman/8.0/en/spatial-geohash-functions.html, (retrieved 20.04.2018)
[5] Donaldson S., Siegel S., Successful Software Development, Prentice Hall Professional, 2001, p.354, https://books.google.bg/books?id=lrix5MNRiu4C
[6] Petrov P., Vazmozhnosti za usavarshenstvane na geokodirashtata sistema Geohash. Sbornik s dokladi ot VIII mezhdunarodna nauchna konferentsia Ikonomikata v promenyashtia se svyat − natsionalni, regionalni i globalni izmerenia (IPS-2017), Varna: Nauka i ikonomika, 2, 2017, pp. 207-212
[7] Hastings C., Wayward J., Wong J., Approximations for Digital Computers, Princeton University Press, 2015, p.159 https://books.google.bg/books?id=IRTWCgAAQBAJ/ (retrieved 20.04.2018)